第25号  計算の雑学  

暗算でポジティブに？

まずは面白雑学的な話からです。洋画で主人公が緊張した時に、簡単な暗算をして心を落ち着かせようとするシーンを見たことがありますが（そんなの見たことないとおっしゃる方もいらっしゃると思いますが・・・）、暗算で本当に落ち着くのでしょうか？　２０１６年に米国のデューク大学にて、こんな興味深い研究があったそうです。

学生を集めて、ＡとＢの２つのグループに分け、両グループとも不安を感じる環境におき、Ａのグループには簡単な暗算（１００から３づつ引いていく）をしているように指示し、Ｂグループには特に何も指示しませんでした。Ａグループの方が不安が少なくなっていたという結果ですが、単に暗算で「気が紛れた」ということではないそうです。Ａグループを分析すると、暗算がうまい生徒ほど不安が少なくなっており、脳の感情をコントロールするエリアが活性化していたそうです。更に調査する学生の範囲を広げて分析してみると、暗算がうまくできる学生ほど、日常生活において不安や心配などのネガティブな感情が少ないことが分かりました。なぜでしょう？　・・・同チームのコメントによると、「感情コントロールと暗算で使う脳のエリアは同じ。そのため、頭の中で計算する能力は、複雑な感情をコントロールする能力とつながっている」そうです。不安な時になれば暗算をすれば少しはポジティブになれるし、暗算力を鍛えれば、普段から不安に対抗できるポジティブな性格になるということでしょう。

言われてみると、生徒は、中級までは「検定落ちたらどうしよう」、「お母さんに怒られる～」、「頑張ってもどうせ・・・」と不安がったり、ネガティブに捉える生徒が必ず一定割合いますが、上級の生徒は皆、そんなことは言わず、落ち着いて集中しています。元々落ち着いてるから上級にいけたのか、暗算力を鍛えるとともに落ち着いてきたのか、と言えば後者のような気もします。まあ、成果を重ね自信が付いた、集中力を鍛えた結果など、他の視点、要素も多くあると思いますが、私たちも知らなかった暗算力を鍛える効果がまだあったというのは嬉しいです。こうなったら、当校のキャッチコピーを「短期間でポジティブになる！」と変えようかと思うのですが、いかがでしょうか？　・・・冗談です。

他にもこんな調査があります。２０１０年同国テキサス大学ですが、「暗算をすると食欲が抑えられる」というものです。一時的に脳の力を計算に回すことで、食欲のシステムが弱るそうです。これは、一時的だから、その後にもっとお腹がすくような気もしてやる気も起きないように思えますが、この際、思いきって、当校のキャッチコピーを「短期間でダイエット！」にするのは有りですかね？　・・・いや、無いですよね。すみません。

なぜ「わり算」が苦手な人が多い？

次は少し真面目な話です。計算は大きく４種類で、まとめて「四則演算」と呼びますよね。「＋－×÷」ですが、この中で一番苦手な計算は？と聞くと、ワースト１位はおそらく「わり算」だと思います。これは、そろばんを習ってる人でも同じ傾向です。なぜわり算が苦手なのでしょうか？その理由を知れば、少しスッキリするかもしれません。一緒に紐解いていきましょう。計算へのご理解も深まると思います。大きく３つの理由があると考えています。

苦手な理由①

一つ目は、「わり算は、四則演算全てを使う」ということです。ちょっと分かりにくいと思いますので、順に説明します。

まず、「足し算」から。気付いている人は少ないのですが、実は、繰り上がりの「足し算」には、「引き算」が必要です。そろばんを使わないやり方で確認してみましょう。やり方は人それぞれですが、たとえば、〔８＋３〕だと、足す数の〔３〕を〔２と１〕に分けて、〔（８＋２）＋１〕で〔11〕と答えを出す人が多いと思います。その場合、８と足して10になる数＝２が必要なので、３から２をひいて１を出していますよね。実際は数の組み合わせを覚えているので、ひき算の感覚すら無いのですが、指折り数える方法以外では引き算が必要です。また、繰り下がる「引き算」をする場合は逆に「足し算」を使います。だから、そろばんでは、このように足し算と引き算は相互補完の関係にあるので、２つ合わせて「みとり算」と呼んでいます。

次に「かけ算」は分かりやすいのですが、九九より大きな「かけ算」をするには、必ず「足し算」をしますよね。筆算でやってもそろばんでやっても同じです。そして、「わり算」ですが、もうお分かりかと思いますが、これまで出てきた計算全てが必要です。

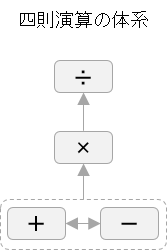
このように「わり算」は四則演算の頂点に位置付けられます。だから、手順が多いし、わり算以前の計算（＋－×）で一つでも苦手な計算があると、わり算はもっと苦手に感じるということです。

そろばんにおいても、わり算で誤答が多い生徒を見ると、わり算以前のみとり算やかけ算で誤答しやすい変なクセが付いていることはよくあります。それを補正すれば、わり算ができるようになるのは基礎的な指導ノウハウです。

苦手な理由②

二つ目は、わり算だけは、スッキリした答えに辿り着かないことがある「わり切れない」計算があることです。例えば、10÷３だと、答えが、３あまり１、または、小数点以下まで求めようとしたら、３．３３３３３・・・・と永久に続くため、どこかで四捨五入しなければなりません。誰しも「計算とはスパッと答えが出るもの」という印象を持っていますが、何かこうスッキリしない感じがします。また、１より小さい数でわるとわられる数より大きくなったり、更に、０でわると無限大、それを電卓でやるとエラーになったりと、（＋－×）と比べると、納得できないというか、とっつきにくいことが多くあるため、わり算は悪い印象になりがちだと思います。以前もご説明しましたが、数学や物理になって高度になればなるほど、分数で処理するようになります。たしかに、分数で示せば、このようなことは解消されたり、理解しやすかったりします。とは言え、わり算は絶対に欠かせない、身に付けなければならない計算の一つです。

日商検定の問題仕様では、そろばんのわり算は、4級までは必ずわり切れ、３級以上がわり切れず、四捨五入する問題が出ます。「あまり」も「小数点以下」もそろばんで問題無くできるのですが、暗算で小数点以下を求めるのは実用的とは言えず、珠算と暗算の関係の視点では、スッキリしない所です。

これらを踏まえ、そろばんでどこまで、どう指導し、何を習得すれば、勉強をはじめ、実生活で本当に役立つものになるのか、日々検討しています。

苦手な理由③

最後の三つ目は、わり算だけは、計算手順が逆ということです。これも言われてみないと気付かないようなことですが、一番大きな要因と考えています。先にわり算以外の計算手順を見てみましょう。筆算で書きます。

このように、（＋－×）は上から下に順に計算して答えに辿り着きます。そろばんも筆算も同じです。ただ、そろばんでは大きな桁から計算するなど、やり方は異なるのですが大きな流れは同じです。一方、わり算はこうです。

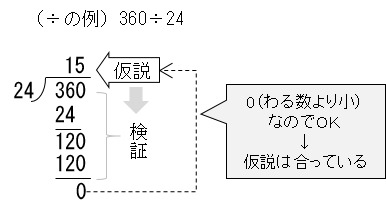
わり算だけは、最初に答えを「仮に」置きます。計算作業はその「仮の答え」が合っているかどうかを確認する検証作業で、間違っていたらやり直しますよね。このように絵にすると分かるのですが、四則演算の中で、わり算だけは解き方が、「仮説検証型」の手順なのです。そろばんも筆算も基本この手順は同じです。そろばんで身に付けるのは、その「仮の答え」が大きい桁でも、訓練によって一発で正確に出せる「確商」というやり方です。

「仮説検証」とは、論理的思考の手法の一つですが、わり算を最初に習う年齢で、「わり算だけは仮説検証型の解き方だから」と断片的に教えてもあまり意味がないですよね。しかし、多くの生徒は、なんとなく「何か今までと勝手が違う」と感じるようで、わり算のやり方を覚えることよりも、慣れることに時間を要し、苦手意識が出てきてしまうことも少なくないと思います。また、この手順が理解できていなければ、検証の計算のひき算をやっている途中でも「仮の答えが違う」と分かれば、そこで止めていいのに、ひき算を最後まで続け、もう一度「仮の答え」を立て直し・・・、と繰り返すことで、とても面倒な計算だと印象付いてしまうこともあります。

まとめ

以上の３つがそろばんに限らず、「わり算が苦手」な要因と私たちは分析しています。最後に、私たち指導する側の視点ですが、特に③が厄介です。わり算には「論理的思考」の要素が少なからず入っていることです。当校では、そろばんの計算は、考えずに反射で、つまり、「直観的思考」で処理するものとして指導し、身体で覚える訓練で習得させるのが基本方針です。わり算においても、強引な方法では無く、「直観的思考」で処理できるような習得法を整える必要があると考え、「直観的思考」だけで処理できるよう改善を重ねてきました。そのため、昨年末以降だけでも、テキストの改訂を実は２回行っていますが、かなりの完成度、納得できる形になったと自負しています。