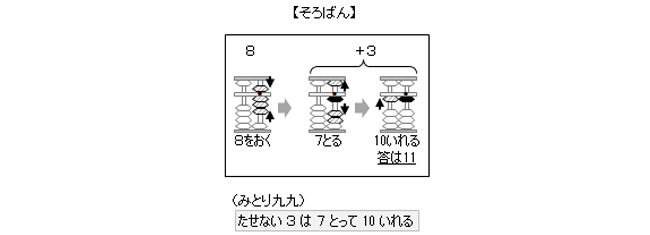
一方、そろばんで8+3はこのように計算します。
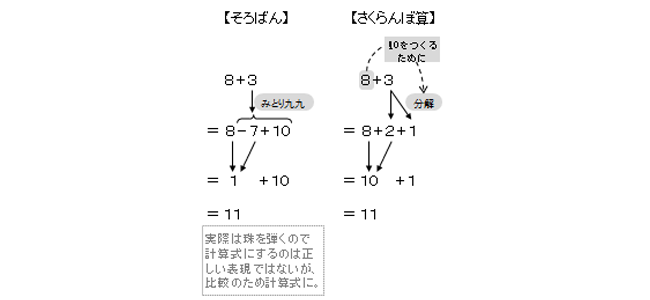
ここで、計算方法のどこが違うのか、どっちの計算がいいか、などをご説明するつもりはありません。計算そのものに焦点を合わせると、混乱の原因を特定することから遠のくことになります。別の視点で見る必要があります。
【補足】 なぜそろばんでは「たす数」だけに注目?
本テーマには直接関係しないのですが、そろばんの計算法の話です。8+3の例のように、そろばんは足される数ではなく、足す数だけを見ます。それには理由があります。それは、桁数・口数がいくら増えても同じように計算するためです。口数とは、8+3なら2口、8+3+2なら3口といったように足す回数を表す言葉です。もし、足される数の方も考慮する計算法ならそうはいかないですよね。だから、12級で一度基礎のやり方さえ覚えれば無限の桁と口数を扱えるのです!
本テーマには直接関係しないのですが、そろばんの計算法の話です。8+3の例のように、そろばんは足される数ではなく、足す数だけを見ます。それには理由があります。それは、桁数・口数がいくら増えても同じように計算するためです。口数とは、8+3なら2口、8+3+2なら3口といったように足す回数を表す言葉です。もし、足される数の方も考慮する計算法ならそうはいかないですよね。だから、12級で一度基礎のやり方さえ覚えれば無限の桁と口数を扱えるのです!
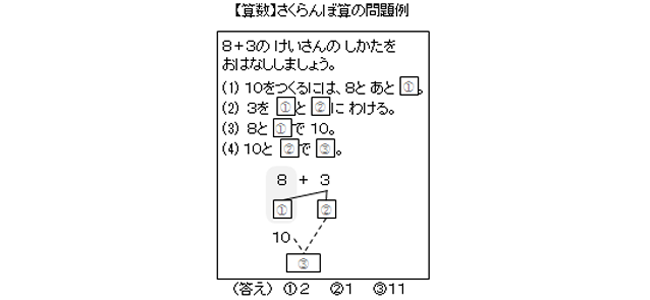
この論理的思考、学年が進むと、それを活用する問題が増えます。算数で代表的なのは、苦手な人が多い「証明」問題、「○と◎が等しいことを証明せよ」みたいなのがそうですが、それだけじゃなく、論理的思考力を問われる問題はとても多くあり、学年が進むほど、その割合は増えていきます。 【さくらんぼ算】のような□を埋める問題の多くは論理的思考が問われる問題です。 1年生で習うこの【さくらんぼ算】 は論理的思考の入門編とも言えます。
【補足】 算数で求められるもの (文部科学省)
文部科学省が何を重視しているかは、ホームページでも指導要領等が公開されているので是非一度、ご覧いただきたいのですが、身に付けるべき、としているスキルは多岐にわたります。その中で、「知的活動(論理や思考)」という言葉が何度も出てきます。論理思考をかなり重視しているのは明らかです。
論理思考の土台は、言葉を正しく扱えることです。算数と言えども、計算力だけではなく、総合的な基礎学力、「読み書きそろばん」が重要ということですね。
文部科学省が何を重視しているかは、ホームページでも指導要領等が公開されているので是非一度、ご覧いただきたいのですが、身に付けるべき、としているスキルは多岐にわたります。その中で、「知的活動(論理や思考)」という言葉が何度も出てきます。論理思考をかなり重視しているのは明らかです。
論理思考の土台は、言葉を正しく扱えることです。算数と言えども、計算力だけではなく、総合的な基礎学力、「読み書きそろばん」が重要ということですね。
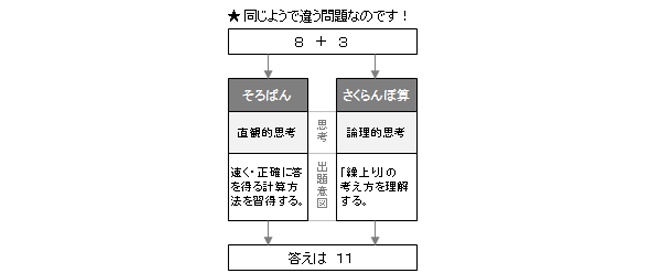
「論理的思考」と「直観的思考」は思考の種類であり、どちらが優れているとかではないです。ただ、思考にこのような違いが存在することを知っていることはとても大切なことです。そして、思考する対象によって適切に使い分けることができれば、強力な武器にもなり得ます。
また、小学校(正確には担任の先生)によって教え方にかなりのバラつきがあるようです。中には、教科書では1問しか出てこないこの【さくらんぼ算】をノート何ページにもわたり練習させ、「計算方法」として手順まで定着させるところもあるようです。それは明らかに違うとは思いますが、最近だと、学校で習う時期まで繰上りを知らない生徒の方が稀で、計算力も個人差が大きいため、「知らない生徒に合わせる」という方針でそのような指導になるのかもしれませんし、論理的思考のトレーニングを重視しているのかもしれません。いずれにしても、ここで小学校毎の指導法の差を論じても仕方がありません。
これを踏まえると、混乱を回避するのは実はすごく簡単なことです。題名に「魔法の言葉」と大げさに書きましたが、実際は魔法など必要ありません。そのまま生徒に伝えればいいのです。「さくらんぼ算とそろばんは答が同じでも違う問題。さくらんぼ算は考えながら解いて、そろばんは考えずにやり方を覚える。両方とも大事。」とさえ言えば、その途端に混乱は納まり、どちらもできるようになります。これは生徒の立場に立って見ればよく分かります。同じたし算なのに違うやり方を教わり、無意識ですが、何とかそれを自分の中で統合しようとし、混乱していたのです。最初から別物と判断する生徒は混乱しないし、そうでない生徒も「気付き」を与えればすんなり納得します。少し種類は違いますが、似たような「気付き」の例で「答合わせ」があります。珠算も暗算も上級なのにやたら合計点を出すのに時間がかかる生徒がいます。「その計算力なら一瞬なのに、なぜ?」と思って見ると、合計を出すのにそろばんを習う前の方法で計算していたりするのです。
【さくらんぼ算】のような例は他にも多くあります。一度でも「気付き」があれば、その後は別の問題でも混乱に陥ることは無いのですが、それまでは生徒からすれば厄介な問題です。指導する側がそれを理解し、適切なタイミングで「気付き」を与えることが有効ですが、現実問題として、私たちが生徒の算数の学習状況まで正確に理解するのは無理があります。もちろん、できる限り把握に努めてはいますが、保護者様にも、この違いをご理解いただければ、その認識が何らか有効に働くのではないかと思い(ご家庭で指導してくださいということではありません)、今回のテーマを取り上げることとしました。